Definición.- Un ángulo es la porción
de plano comprendida entre dos semirrectas que se cortan en un punto denominado
vértice a las semirrectas se le llama lados.
Para designar a los ángulos se utilizan tres letras dos para los
lados y uno para el vértice que se coloca en medio AOB,
o bien con una sola letra colocada en el vértice O,
con una letra (normalmente del alfabeto griego) en el interior del ángulo
y al lado de un arco de circunferencia que va de un lado a otro, con centro
en el vértice a.
Ángulo cóncavo y convexo.- Las semirrectas OA y OB además de definir el ángulo convexo a, también definen el ángulo b, cóncavo. Salvo indicación contraria nos referiremos siempre al ángulo convexo.
Ángulo llano es el formado por dos semirrectas que están en prolongación una de otra.
Ángulos orientados.- Diremos que un ángulo está orientado en sentido positivo, si dicho ángulo se "barre" del lado OA al lado OB, en sentido contrario a las agujas del reloj. En caso contrario se dice de sentido negativo.
Ángulos iguales.- Dos ángulos se dicen iguales si mediante un movimiento los podemos superponer.
Los llamaremos directamente iguales si además de iguales tienen el mismo sentido.
Ángulos consecutivos.- Dos ángulos se dicen consecutivos cuando tienen el mismo vértice, un lado común y el otro lado lo tienen situado en distinto semiplano del lado común.
Ángulos adyacentes.- Dos ángulos consecutivos se dicen adyacentes si tienen los lados no comunes en línea recta.
Ángulo recto es la mitad de un ángulo llano, o bien dos adyacentes iguales, también podemos decir que es formado por dos semirrectas perpendiculares.
Ángulos complementarios son los que suman un ángulo recto, y ángulos suplementarios son los que suman un ángulo llano.
Ángulos opuestos por el vértice.- Dos ángulos se dicen opuestos por el vértice cuando los lados de uno son prolongación del otro.
Bisectriz de un ángulo.- Se llama bisectriz
de un ángulo a la semirrecta que divide un ángulo en dos
partes iguales.
Para obtener la bisectriz de un ángulo BAC, trazamos con centro
A un arco de circunferencia que corte a los lados en D y E. Con centro
D y radio cualquiera E, trazamos una circunferencia, y con el mismo radio
trazamos otra desde E. El punto de corte de ambos circunferencias nos
da un punto F, uniendo dicho punto con el vértice obtenemos la
bisectriz.
Ejercicio.- Demuestra que las bisectrices de ángulos adyacentes son perpendiculares. Solución.
Ejercicio.- Demuestra que los ángulos opuesto por el vértice tienen las bisectrices alineadas. Solución.
Ángulos colaterales, correspondientes, alternos-internos, alternos-externos.
Dada una recta que corta a otras dos, determina ocho ángulos, cuatro con cada una de ellas. Cuatro internos y cuatro externos.
Son internos los comprendidos por las rectas a y b, a un lado y otro de la secante c, como III, IV, V y VI; y externos los que están fuera de dichas rectas a ambos lados de la secante, como son I, II, VII y VIII.
Se dicen colaterales los ángulos situados al mismo lado de la secante como son: III y V, I y VII, IV y VI, II y VIII.
Se llaman alternos-internos dos ángulos internos no colaterales ni adyacentes, como son III y VI, IV y V.
Se llaman alternos-externos, dos ángulos externos y no colaterales ni adyacentes, como son II y VII, I y VIII.
Diremos que dos ángulos son colaterales internos, o internos del mismo lado, también se le llaman conjugados a dos ángulos colaterales e internos, cocos son IV y VI, III y V.
Y se llaman colaterales externos o externos del mismo lado a los ángulos que son colaterales y externos, tales como I y VII, II y VIII.
Actividad.- Traza dos rectas paralelas y una secante, comprueba y demuestra que:
- Los ángulos alternos-internos son iguales.
- Los ángulos alternos-externos son iguales
- Los ángulos correspondientes son iguales.
- Los ángulos colaterales internos son suplementarios.
- Los ángulos colaterales externos son suplementarios.
Recíprocamente si se da uno de los casos 1,2,3, 4 o 5 las rectas son paralelas. Para demostrarlo basta suponer que las rectas no son paralelas, trazar una paralela por el punto de corte de la secante y los ángulos alternos-internos que se formarían serían iguales y coincidentes con los dados, por tanto la recta a y la paralela trazada serían iguales.
Problema.- Halla la suma de los ángulos de un triángulo.- Solución.
Un ángulo exterior de un triángulo es el formado por un lado y la prolongación de otro.
Problema.- ¿Cuánto suman los ángulo exteriores de un triángulo?¿Y de un polígono cualquiera?
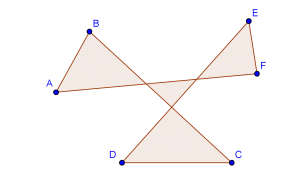
Problema.- Halla la suma de los ángulos A+B+C+D+E+F
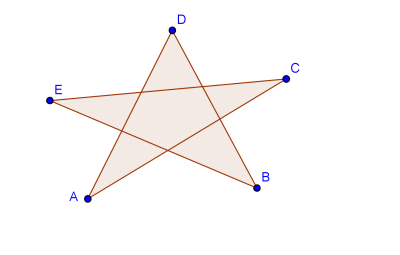
Problema.- Halla la suma de los ángulos de vértices A+B+C+D+E de la estrella de cinco puntas
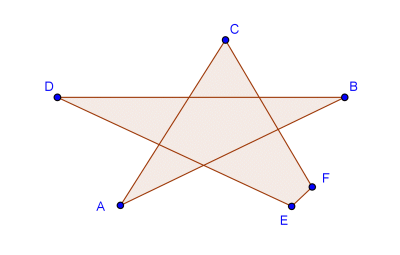
Problema.- Halla la suma de los ángulos de vértices A+B+C+D+E+F
Problema.- Halla la suma de los ángulos de un polígono convexo de n lados. Solución
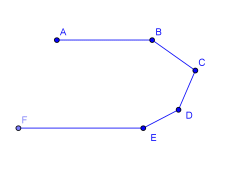
Problema.- Sabiendo que AB es paralela a EF, halla la suma de los ángulos de vértices B+C+D+E
Problema.- ¿Cuánto vale la suma de los ángulos ACH+ADH de la figura siguiente?
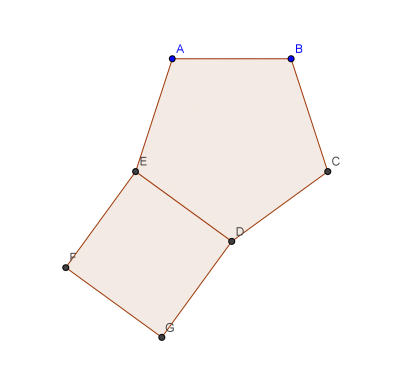
Problema.- DEFG es un cuadrado que se ha trazado fuera del pentágono regular ABCDE. ¿Cuánto mide el ángulo EAF?
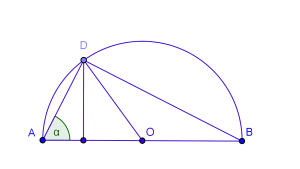
Problema.- Calcula el valor de los nueve ángulos restantes en función de alfa.
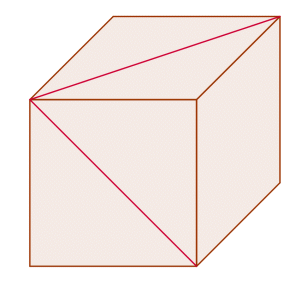
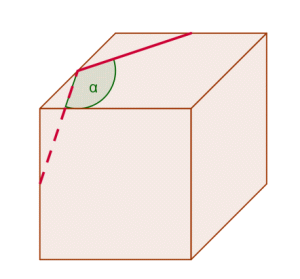
Problema.- ¿Cuántos grados mide el ángulo que forman las dos diagonales de las caras del cubo?
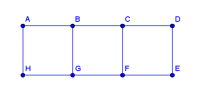
Problema.- ¿Cuánto mide el ángulo obtuso ABC? A, B y C son los puntos medios de los lados.
Problema.- Dado el cuadrilátero cóncavo de la imagen, demuestra que a+b+c=d. Solución
Problema.- Demuestra que la suma de los ángulos dibujados en verde coincide con la suma de los pintados de rojo, sabiendo que están comprendidos entre dos paralelas. Solución
Problema.- Calcula el valor del ángulo que determinan las bisectrices de los ángulos A y H.Solución
Observa, en el siguiente applet las rectas son paralelas. ¿cuánto vale la suma de los ángulos?
Problema.- ¿Cuánto vale la suma de los ángulos externos de un polígono convexo?
Problema.- ¿Qué ángulo forman las agujas del reloj a las cinco menos cuarto?¿Y a las cinco menos veinte?
Actividad.- Comprueba y demuestra que los ángulos que tienen sus lados paralelos son iguales o suplementarios. Solución.
Actividad.- Comprueba y demuestra que dos ángulos que tienen
sus lados perpendiculares son iguales o suplementarios. Solución
Observemos que si los ángulos son ambos agudos u obtusos son iguales,
si uno es agudo y el otro obtuso entonces son suplementarios.
Problema.- Sabiendo que las rectas c y e son paralelas, ¿cuánto mide el ángulo beta?
Medida de ángulos.Arcos y cuerdas. Ángulos en la circunferencia.Teorema de Thales. Homotecia y semejanza. Trigonometría. Razones trigonométricas de un ángulo agudo. Razones trigonométricas de ángulos cualesquiera. Relación fundamental. Secante, cosecante y cotangente. Reducción al primer cuadrante. Razones trigonométricas de ángulos complementarios. Razones trigonométricas de la suma o diferencia de dos dados. Razones del ángulo doble y mitad. Funciones circulares. Ecuaciones trigonométricas. Resolución de triángulos. Teorema de Pitágoras. Teorema de altura. Teorema del seno. Teorema del coseno. Coordenadas. Vectores. Recta en el plano: generalidades. Ecuaciones de la recta. Incidencia y paralelismo. Distancia punto recta.. Funciones:generalidades. Dominio. Simetría y periodidcidad. Crecimiento. Operaciones con funciones. Función polinómica. Funciones a trozos. Funciones trascendentes.
