Las funciones están presentes en todo lo que nos rodea, incluso en nuestro organismo, por ejemplo las pulsaciones nos indican lo rápido que late nuestro corazón.
El número de pulsaciones depende de varios factores, entre ellos la edad, si estas en reposo o haciendo ejercicio, también depende de la constitución y de la condición física, etc.
La velocidad de la marcha en bicicleta depende del terreno y de como pedalees, la distancia que recorres depende de la velocidad y del tiempo empleado.
El salario de los trabajadores depende de las horas trabajadas, de la cualificación,.....

El valor de una vivienda, depende de su situación, metros cuadrados, calidad de la construcción, etc.
El texto que estas leyendo depende de la resolución aplicada en tu monitor.

Veamos algunos ejemplos más concretos.

  • El área de un triángulo es S = [(b·h)/2], observemos que el área depende de dos variables independientes la base y la altura. El área diremos que es la variable dependiente y la base y la altura son las variables independientes.
  • El área de un triángulo equilátero es S = [(a2 Ö3)/4], ahora el área depende únicamente de una variable el lado a.
  • El espacio recorrido por un vehículo depende de la velocidad y del tiempo.
    e=v·t
    en este caso la velocidad v y el tiempo t son las variables independientes y el espacio e es la variable dependiente.
  • La clasificación de la 1ª división de fútbol depende de los resultados obtenidos, es decir, de los partidos ganados y empatados. La posición es la variable dependiente y los resultados anteriores la variable independiente.
  • También una función puede venir dada por una gráfica


 

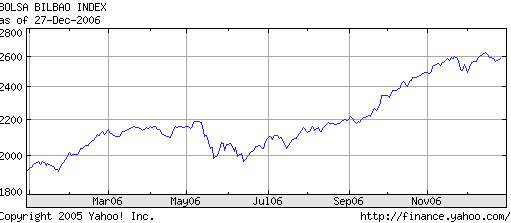
Correspondencia

Sean A y B dos conjuntos, se define una correspondencia como un subconjunto del producto cartesiano A×B.

Ejemplo.- Sea A={1,2} y B={a,e,i,o,u} el producto cartesiano es el conjunto

A×B={(1,a),(2,a),(1,e),(2,e),(1,i),(2,i),(1,o),(2,o),(1,u),(2,u)} y un subconjunto puede ser C={(1,a),(1,e),(2,i),(2,u),(2,o)}, que esta definido por extensión (dando todos los elementos del conjunto) y se podría haber definido por comprensión (dando una propiedad que sólo verifican los elementos del conjunto) C es la correspondencia que asocia al 1 las vocales fuertes y al 2 las débiles. En la correspondencia C se dicen que los elementos 1 y a son homólogos, al igual que 1 y e, etc.

Una aplicación es una correspondencia donde a todo elemento del primer conjunto le corresponde un único elemento del segundo conjunto.

Observando el ejemplo anterior podemos deducir que C no es una aplicación, observemos que al 1 le corresponde más de un elemento del segundo conjunto.

Ejemplo.- Sea X={(1,a), (2,a)} un subconjunto de A×B dados en el ejemplo anterior. Veamos que X es una aplicación.
Todos los elementos de A tienen homólogo.

A cada elemento de A le corresponde un único elemento de B.

OBSERVACIÓN.- Que a cada elemento de X le corresponda un único elemento no quiere decir que este sea el mismo como ocurre en el ejemplo anterior.

Ejemplo.- Sea Y = {(1,a),(2,u)}. A cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto, al 1 le corresponde la a y al 2 le corresponde la u.

Ejercicio.- Observa la figura siguiente, mueve el punto E, consideramos la correspondencia que asigna a cada punto del diámetro de la circunferencia los puntos Fy G, ¿es aplicación? Razona la respuesta.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

Ejemplo.- Consideramos el conjunto A formado por {Carlos, Paco, Javi, Elena} sabemos que Carlos tiene 17 años y pesa 71 kg., Paco tiene 16 años y pesa 61 kg, Javi tiene 18 años y pesa 81 kg y por último Elena tiene 15 años y pesa 51 kg. Si a cada elemento del conjunto A se le hace corresponder su edad, ¿será aplicación la correspondencia así definida? Dibuja una gráfica que represente dicha correspondencia.

Carrera de F1.- Indica como varía la velocidad cuando recorre cada uno de los circuitos


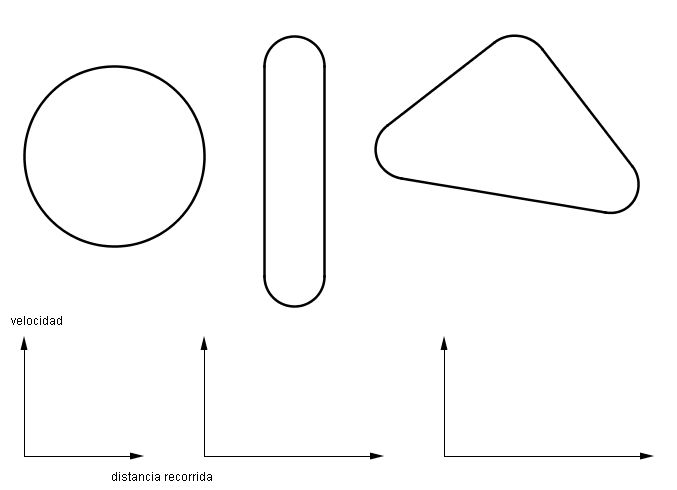
Responde razonadamente a las siguientes cuestiones:

  • ¿Qué curva es más peligrosa?
  • ¿Cuál es la recta más larga del circuito?
  • ¿El coche empieza la segunda, tercera vuelta,... con la misma velocidad que la primera?
Si los conjuntos A y B son numéricos a la aplicación se le denomina función, y se suele notar de la siguiente forma:

f : x Î D ® f(x) = y Î R

a D se le llama dominio de la función, a x se le denomina variable independiente y a y variable dependiente. Al conjunto de elementos homólogos de elementos de D se le denomina recorrido.
Se llama gráfica de f al conjunto de puntos del plano definido por G(f)={(x,y)Î R2 / y = f(x)}.

Ángulos. Medida de ángulos.Arcos y cuerdas. Ángulos en la circunferencia.Teorema de Thales. Homotecia y semejanza. Trigonometría. Razones trigonométricas de un ángulo agudo. Razones trigonométricas de ángulos cualesquiera. Relación fundamental. Secante, cosecante y cotangente. Reducción al primer cuadrante. Razones trigonométricas de ángulos complementarios. Razones trigonométricas de la suma o diferencia de dos dados. Razones del ángulo doble y mitad. Funciones circulares. Ecuaciones trigonométricas. Resolución de triángulos. Teorema de Pitágoras. Teorema de altura. Teorema del seno. Teorema del coseno. Coordenadas. Vectores. Recta en el plano: generalidades. Ecuaciones de la recta. Incidencia y paralelismo. Distancia punto recta.. Dominio. Simetría y periodidcidad. Crecimiento. Extremos relativos. Operaciones con funciones. Función polinómica. Funciones a trozos. Funciones trascendentes.