| Esquema práctico |
Los problemas de programación lineal pueden presentarse en la forma estándar, dando la función objetivo y las restricciones, o bien plantearlos mediante un enunciado. Si éste es el caso, puede seguirse el camino que indicamos a continuación, ejemplificado con el siguiente problema:
En un almacén se guarda aceite de girasol y de oliva. Para atender a los clientes se han de tener almacenados un mínimo de 20 bidones de aceite de girasol y 40 de aceite de oliva y, además, el número de bidones de aceite de oliva no debe ser inferior a la mitad del número de bidones de aceite de girasol. La capacidad total del almacén es de 150 bidones. Sabiendo que el gasto de almacenaje es el mismo para los dos tipos de aceite (1 unidad monetaria) . ¿Cuántos bidones de cada tipo habrá que almacenar para que el gasto sea máximo?
| Obs: Puede parecer algo absurdo maximizar los gastos , pero se ha enunciado de esta forma para que el ejemplo sea lo más completo posible |
Paso 1º: Leer detenidamente el enunciado: determinar el objetivo, definir las variables y escribir la función objetivo.
El objetivo es: halla cuántos bidones de cada tipo hay que almacenar para maximizar los gastos
Suponemos que tal objetivo se consigue almacenado x bidones de aceite de girasol e y de aceite de oliva
Cómo cada bidón de aceite de girasol cuesta almacenarlo 1 unidad monetaria y lo mismo para uno de aceite, los gastos serán x + y
Luego, la función objetivo es:
Maximizar la función Z = f(x,y) = x + y
Paso 2º: Reordenar los datos del problema y a partir de las cantidades decididas, x e y, escribir el sistema de inecuaciones que determinan las restricciones.
Además, los números
de bidones deben ser cantidades positivas: x
![]() 0 ; y
0 ; y
![]() 0
0
| Obs.: Como veremos en ejemplos posteriores en algunas ocasiones puede interesar utilizar una tabla para recopilar toda la información y hacer los dos primeros apartados |
Paso 3º: Expresar el problema en la forma estándar.
Siguiendo con el ejemplo, sería:
| Maximizar: | Z = f(x,y) = x + y |
| sujeto a: | x + y |
| y |
|
| x |
Aquí termina el planteamiento del problema. Para su resolución hay que continuar con :
 Paso
4º: Representar
gráficamente las restricciones y marcar claramente la región
factible.
Paso
4º: Representar
gráficamente las restricciones y marcar claramente la región
factible.
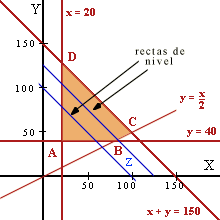
Para las restricciones anteriores debemos representar las rectas: x + y = 150 , y = x/2 , x = 20 e y = 40, obteniéndose la región factible que en la figura se encuentra coloreada.
Paso 5º: Hallar las coordenadas de los vértices del polígono obtenido.
Resolviendo los sistemas : { x = 20, y = 40 } , { y = x/2 , y = 40 } , { y = x/2 , x + y = 150} , { x + y = 150, x = 20}; se obtienen los vértices: A(20,40) , B(80,40) , C(100, 50) , D(20,130)
Paso 6º: Sustituir las coordenadas de esos puntos en la función objetivo y hallar el valor máximo o mínimo.
Sustituyendo en f(x,y) = x + y, se tiene:
f(20,40) = 60 , f(80,40) = 120 , f(100, 50) = 150 , f(20,130) = 150
Como el valor máximo se obtiene en los puntos C y D, puede optarse por cualquiera de los dos, o por cualquier punto perteneciente al segmento que los une. Así, por ejemplo, se obtendría el mismo gasto con 40 bidones de aceite girasol y 110 bidones de aceite de oliva; o 90 y 60 respectivamente.
Paso 7º: También es conveniente representar las rectas de nivel para comprobar que la solución gráfica coincide con la encontrada. Esta conveniencia se convierte en necesidad cunado la región factible es no acotada.
En nuestro caso,
puede comprobarse que las rectas de nivel tienen la misma
pendiente que la recta límite de la restricción x + y ![]() 150 ; por tanto, hay
múltiples soluciones.
150 ; por tanto, hay
múltiples soluciones.
Paso 8º: Por último, como en la resolución de todo problema es necesario criticar la solución: cerciorarse de que la solución hallada es lógica y correcta.
En este ejemplo, no todos los puntos del segmento CD son soluciones válidas, ya que no podemos admitir valores de x e y no enteros , como ocurriría en el punto (90.5,59.5) .
| Obs.: Si un problema en la forma estándar no indica que se debe realizar por el método analítico o gráfico , seguiremos para su resolución los pasos del 4º al 8º |