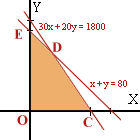| Factibles | Si existe el conjunto de soluciones o valores que satisfacen las restricciones. A su vez, pueden ser: | |
| Con solución única | ||
| En una
urbanización se van a construir casas de dos tipos: A y
B. La empresa constructora dispone para ello de un
máximo de 1800 millones de pesetas, siendo el coste de
cada tipo de casa de 30 y 20 millones, respectivamente.
El Ayuntamiento exige que el número total de casas no
sea superior a 80. Sabiendo que el beneficio obtenido por la venta de una casa de tipo A es 4 millones y de 3 millones por una de tipo B, ¿cuántas casas deben construirse de cada tipo para obtener el máximo beneficio?
Tiene por región factible
la región coloreada.
|
||
| Con solución múltiple | Si existe más de una solución....................................................................................... | |
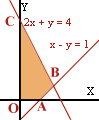 Maximizar la función Z = f(x,y) = 4x +
2y sujeta a las restricciones 2x + y Maximizar la función Z = f(x,y) = 4x +
2y sujeta a las restricciones 2x + y Los valores de la fucnión objetivo
en cada uno de los vértices son:
|
||
| Con solución no acotada | Cuando no existe límite para la función objetivo | |
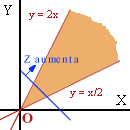 Maximizar la función Z = f(x,y) = x + y
sujeta a las restricciones y Maximizar la función Z = f(x,y) = x + y
sujeta a las restricciones y Tiene por región factible la zona coloreada
que aparece en la figura, que es una región no acotada.
|
||
| No factibles | Cuando no existe el conjunto de soluciones que cumplen las restricciones, es decir, las restricciones son inconsistentes. | |
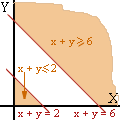 Maximizar la función Z = f(x,y) = 3x +
8y sujeta a las restricciones x + y Maximizar la función Z = f(x,y) = 3x +
8y sujeta a las restricciones x + y No existe la región factible, ya que las
zonas coloreadas que aparecen en la figura son
únicamente soluciones de alguna de las inecuaciones . |
||