6. Tablas de contingencia y diagramas de árbol.

En los problemas de probabilidad y en especial en los de probabilidad condicionada, resulta interesante y práctico organizar la información en una tabla de contingencia o en un diagrama de árbol.
Las tablas de contingencia y los diagramas de árbol están íntimamente relacionados, dado uno de ellos podemos construir el otro. Unas veces, los datos del problema permiten construir fácilmente uno de ellos y a partir de él podemos construir el otro, que nos ayudará en la resolución del problema.

• Conversión de una tabla en diagrama de árbol

  Las tablas de contingencia están referidas a dos características que presentan cada una dos o más sucesos.

  	A		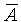TOTAL
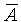
  B	P( A B )	P( B )	P( B )
  	P( A )	P( 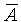)	P( )
  TOTAL	P( A )	P( 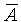)	1

  
  

  En el caso de los sucesos A, 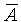, B y , expresados en frecuencias absolutas, relativas o probabilidades la tabla, adopta la forma adjunta.

  
  

  Dicha tabla adopta la forma del diagrama de árbol del dibujo. En éste, a cada uno de los sucesos A y 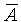se les ha asociado los sucesos B y .

  

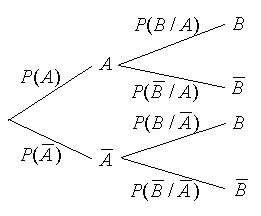
  Sobre las ramas del diagrama de árbol se han anotado las probabilidades condicionadas correspondientes, deducidas de las relaciones análogas a:

  
  

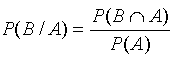
• Conversión de un diagrama en tabla de contingencia

  De manera recíproca, dado el diagrama de árbol podemos construir la tabla de contingencia equivalente si más que utilizar la expresión

  P( BA ) = P( B/A ) · P( A ),
  

  para calcular las probabilidades de las intersecciones de sucesos que forman la tabla.